这是一道五年级附加题，求阴影部分面积，很多学生找不到解题的思路方法，只能干着急。 如图所示，长方形内三角形面积是4和5，求阴影部分面积？ 这道题可以利用一半模型解答题目，通过和长方形面积关系，想办法求出三角形ABF的面积，这道题就简单了。
六年级奥数题，难度非常大，一个班级能答对的学生不到3人，非常考验学生的几何思维能
【4评论】【1点赞】
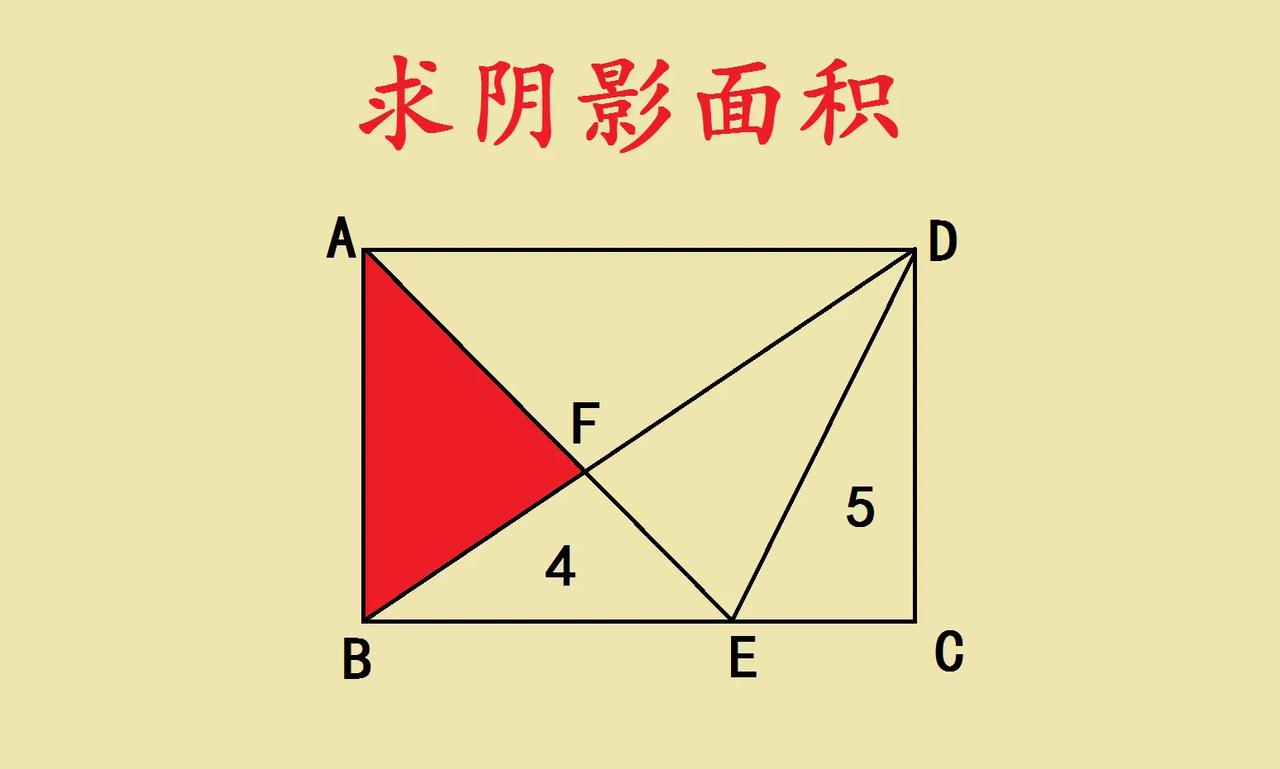
这是一道五年级附加题，求阴影部分面积，很多学生找不到解题的思路方法，只能干着急。
大力小学数学吖
2025-02-26 10:31:08
0
阅读：305
用户10xxx48
6，不用相似。也不算超纲。设同底等边面积为s， 4:s＝s:9， s×s＝4×9＝36＝6×6 s＝6
Locky
通过平行线性质，把面积比化为底高比就能知道阴影△面积。
喂，是你
6
秋风秋雨zwc
6用三角形相似可算出但超纲。
喂，是你 回复 04-09 06:52
要毛的相似，用一半模型和蝴蝶模型
用户2025
4:s=BF:FD=s:9 => s=6